Representing money in many ways: Addition, fractions and equivalents

Help your Grade 3 students make change, understand fractions and represent money in different ways. Use these activities individually or in the order listed in this lesson.

Overview

Big idea

We use different combinations of coins and bank notes to represent the same value.
Money is a common way we use fractions in daily life.

Total time

105 minutes of instruction and math exercise work

Grade level

Grade 3

Subject areas

Math

• calculate the change needed for cash transactions of a whole dollar and amounts less than one dollar
• identify different ways to represent the same amount of money
• model different costs and the change required
• represent and solve fair-share problems using money and equivalent fractions

Learning objectives

Students will:

• use different strategies to determine the value of a combination of coins or bank notes
• represent an amount of money using different combinations of coins and bank notes
• determine how much money is needed for transactions in word and number problems
• identify different denominations of Canadian coins and bank notes

Materials

Classroom supplies and technology

• Pencils
• Printer
• White board and markers (or smartboard or projector)
• Play or real Canadian coins (optional)
• Two dice (optional)

Worksheets

1. Download the activity and answer sheets.
2. Print one copy of the applicable worksheets and graphics for each student:
   • Activity 1: Calculating Change 1 and Calculating Change 2
   • Activity 2: Same Amount, Different Ways and Converting Change
   • Activity 3: Fair Share Fractions and Sharing is Caring

Activity 1: Making change in simple transactions

In this activity, students calculate the amount of money needed for simple transactions and the change given when paying with a larger denomination coin or bank note. The first activity uses whole-dollar amounts, and the second uses amounts less than a dollar.

Hand each student one copy of the worksheets “Calculating Change 1” and “Calculating Change 2”.

Time

30 minutes

1.1 Worksheet activity: Calculating change

Begin with the first page. In each question students will fill in the missing piece of the shopping trip: either how much was paid, how much change was received or what was purchased.

Do the first question together, and then have your students work individually or in groups to complete the next examples. Note that the questions become increasingly difficult with higher costs.

Once students have completed the worksheet, use the answer key to correct together.

Take a moment to review the final question (#5) together. Check if students answered $5. Ask your students why, if the cost was less than $20, the person chose to pay with $22.

Explain to students that sometimes people will pay with more cash than needed so that they receive a bill back instead of extra small coins. If time allows, you may want to practise this together with the following examples:

• If something cost $6 and you wanted a $5 bill back, how much would you pay? ($11)
• If something cost $14 and you wanted $10 back, how much would you pay? ($24)

Show students the pattern: if you want a certain amount of change back, add that amount to the cost to determine how much you need to pay.

Practice whole dollar transactions in the first part of Calculating Change. Then, use the second worksheet for more complicated transactions.

1.2 Worksheet activity: Calculating change

Before starting the second worksheet, show students patterns where they can use skip counting to quickly [add/find a total]. Here are some examples:

• The wrapped bonbons cost 20¢ each. So, students can skip count the same candies in Question 1 of the worksheet (20, 40, 60, 80).
• They can also skip count coins, such as the four quarter coins in Question 1 (25, 50, 75, 100).

For the next activity, explain to students that they will use the same money math skills to provide change in cents for items that cost less than a dollar. In the first column, ask students to add and write the total cost for the candies each person wants. The second column shows how much money each person pays. In the third column, students calculate the change due, write this amount and draw pictures of those coins (such as small circles with the denominations 5¢, 10¢, 25¢, etc.)

To assist with the math, use the following approaches:

• Before adding, write the cost of each candy next to it in the first part of the question.
• Use skip counting to (such as the three snakes in Question 3), then add the cost of different candies.

Once students have completed the worksheet, correct it together.

Activity 2: Introducing fraction and money relationships

In this activity, students work with change to understand money’s relationship to fractions. They also identify patterns to make counting large amounts of money easier.

Time

40 minutes

2.1 Discussion: Money patterns

Discuss with your students the patterns they notice in money.

Ask the following questions to assess prior knowledge. Use skip counting, multiplication and division to help students if they are unsure of the answers.

• How many quarters make up a dollar? How about dimes? Nickels?
• If you received $100 in 20-dollar bills, how many would you have? How about $100 in 10-dollar bills?

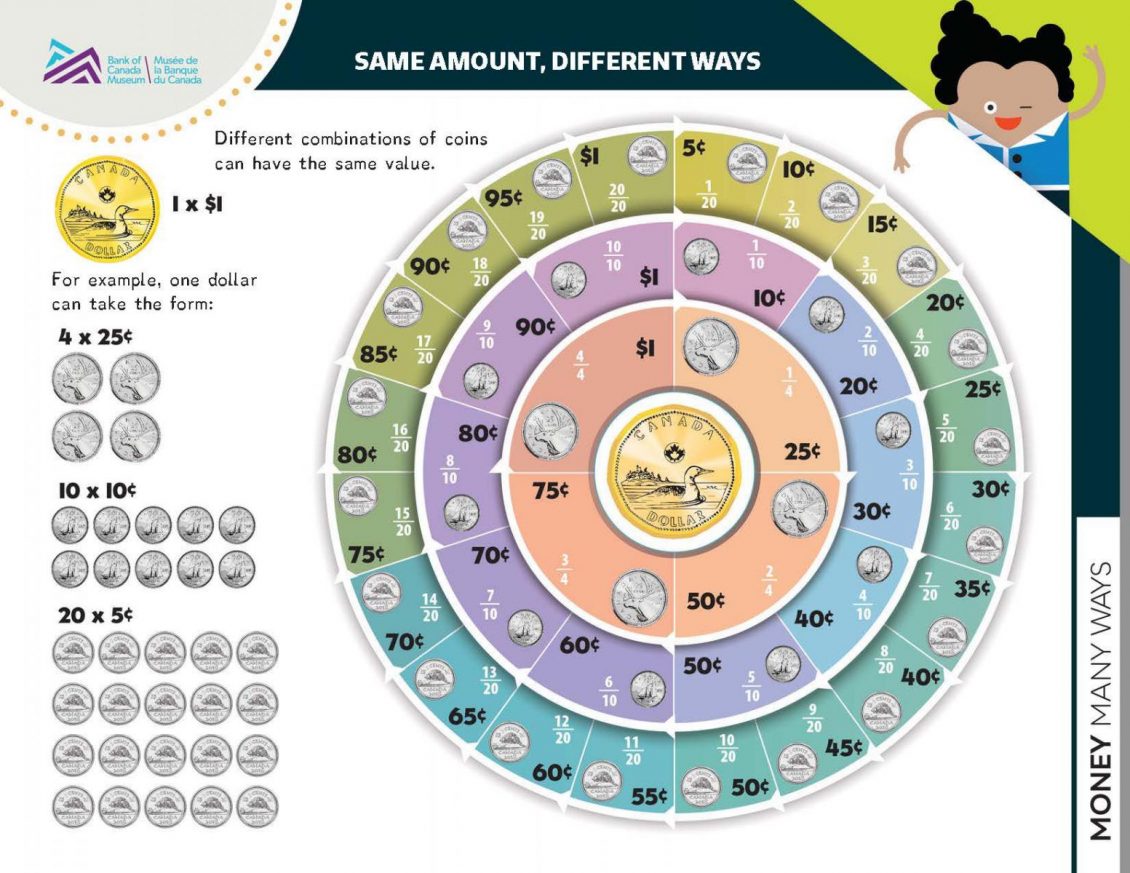
Hand out (or display) the graphic “Same Amount, Different Ways”. Explain to students that this diagram helps to show how the value of one dollar (or 100 cents) can be expressed using different coins. The coins show different fractions of a dollar.

Use the Same Amount, Different Ways illustration to show the relationship between fractions and money.

Show students the different layers of the circle (nickels, dimes and quarters) and how different fractions (or amounts) of a dollar can be displayed.

2.2 Diagram introduction: Same amount, different way

Then, introduce parallel fractions with coin amounts using the pie chart next to the diagram. Show one-half, one-quarter or one-fifth of the pie chart by covering part of the chart with your hand or a piece of paper. Or you could laminate the sheet and use markers or display the pie chart using a smartboard or projector.

As you cover up different sections of the circle, ask your students to help you record the following answers on the white board for each fraction you are exploring:

• the fraction in its simplest form (½, ¼ or ⅕)
• the equivalent fraction with 100 as the denominator (50/100, 25/100, 20/100)
• the number of cents needed for each fraction of a dollar (50¢, 25¢, 20¢)
• the decimal equivalent for each fraction (optional) (.50, .25, .20)

Show your students the relationship between the simple fraction and the equivalent fraction, and that they mean the same thing. For example, if you have a dollar and someone takes half of it, then that 50¢ amount is the same as ½ or 50/100, whether it is shown in a simple fraction or out of 100 cents (a dollar). Instead of saying you have a “quarter of a dollar,” you would normally just say 25¢, or a quarter.

You may want to explore the fraction-based names of Canadian coins to help your students understand their value compared with a dollar. A quarter is clear enough. A dime comes from the Old French word disme and the Latin decima, meaning a tenth. The nickel was originally called a half-dime. While not in regular circulation and rarely used, half dollars—or fifty-cent coins—still exist in both Canada and the United States. Most are collectors’ coins.

If time allows, you may also want to do one of the following activities to help your students count change, to prepare for the next worksheet:

• Use play money coins as manipulatives to count and represent different fractions and amounts. Students can place the play money directly over the diagram to help show the fraction (part of a whole dollar). This can also serve as a skip counting activity. Use our other worksheet activities for more skip counting exercises.
• As a class or in small groups, have your students each call out a number displayed on the diagram along with a coin of that ring (for example, “65¢ in nickels”). Then have students race to be the first to say the correct number of coins needed for that amount.

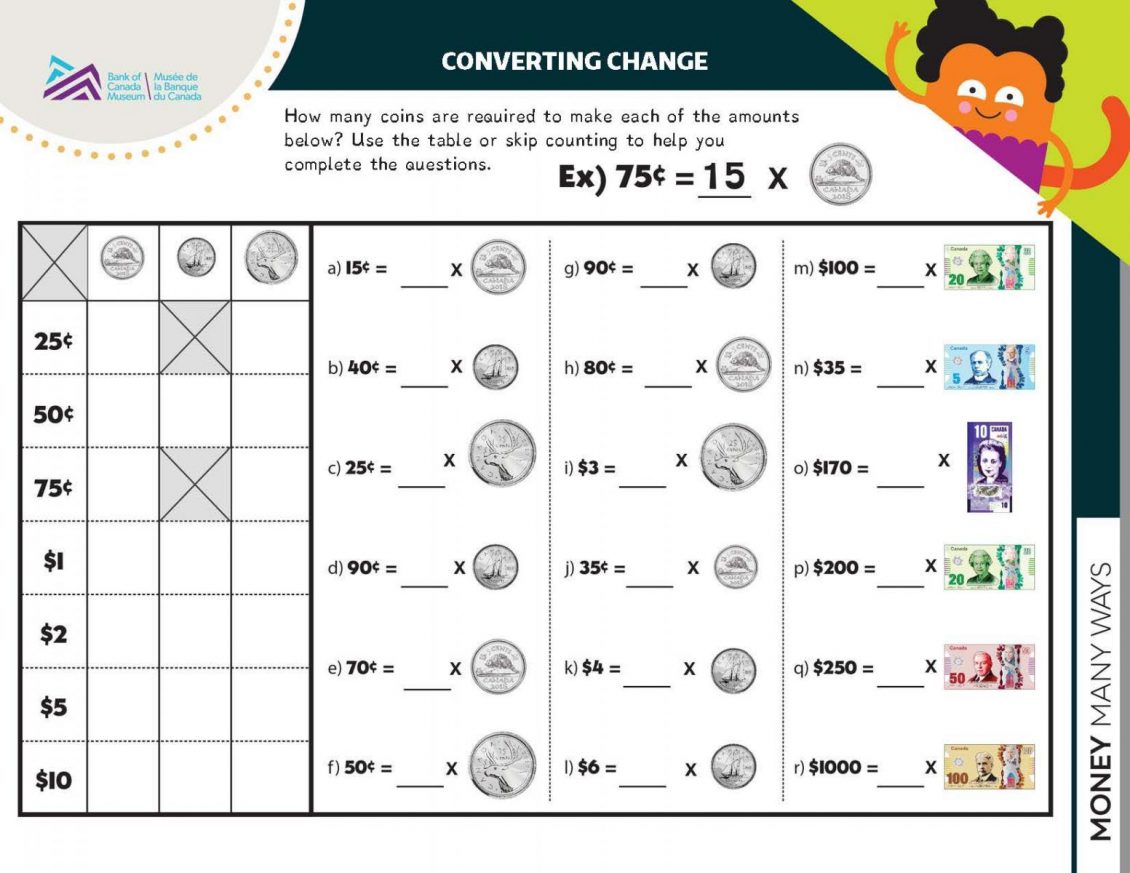
2.3 Worksheet activity: Converting change

Hand out one copy of the worksheet “Converting Change” to each student. Together, discuss the first row of the table in task 1, as an example (i.e., 25¢ can be made from 5 nickels, no dimes or one quarter).

Depending on their needs, have students continue individually or in pairs with the rest of the questions in the table. They can refer to the ring diagram on the previous worksheet for help. If more support is needed, show the following:

• The number of nickels, dimes and quarters needed to make $2 is the same as doubling each of the amounts from the row above (amount required for making $1).
• The number of each type of coin needed to make $5 can be calculated by adding the number in the $2 row twice and then adding the number in the $1 row once.
• The numbers needed for the $5 row can be doubled to make the numbers for the $10 row.
• It’s not possible to make 75¢ from dimes. Explain that a dime (like counting by 10s) will only ever equal a number that ends in 0, no matter how many are added together. If you have already introduced decimals, you may want to use this [example/opportunity] to show a decimal answer (7.5).

Review and correct together.

Use Converting Change to help recognize patterns in change amounts.

Activity 3: Dividing money using fractions

In this activity, students will confirm how much money they need to buy items, and they will represent the same amount of money using different coin combinations.

Time

30 minutes

3.1 Discussion: Evenly dividing money

Before handing out the worksheet, ask students if they have ever seen people split (divide) money into two or three equal amounts. How would they divide money between two people? How would they do it if the amount was, say, a 20-dollar bill? What if the amount to split was five dollars?

Students may offer some examples that match those on the first page of the worksheet “Fair Share Fractions.” Finding change equivalents (or smaller amounts) is a good lead-in to the worksheet activity.

3.2 Worksheet Activity: Fair share fractions and Sharing is caring

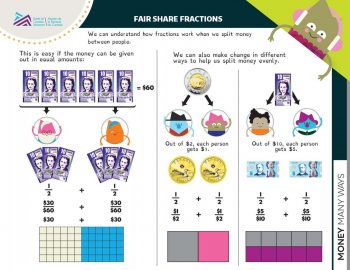
Hand out one copy of the worksheet to each student. Go through the steps of how to split money equally between people. Show students how splitting the amount of money is like making a fraction. The whole amount of money (or 1/1) is equivalent to two smaller, equal amounts when it is split in half.  Fractions show a part of the whole, so when you split something in half, the fraction is 1/2. (Show students that the total number of parts is the bottom number of the fraction, called the denominator. The top number of the fraction is the numerator, which shows how many parts of the whole).

Explain that we can use fractions to show how we divide—or split—money. Since we can’t split one bank note between two people, we can swap that large bill for an equivalent amount in smaller bills. Those smaller bills can then be divided. Go through the example using smaller coins to help divide a toonie.

Help students understand why some amounts divide neatly. For example, ask students the following questions:

• Does $6 divide evenly between two people? (Yes, each person would get $3). What about $4? (Yes, each person would get $2).
• How many loonies would you need to divide fairly among 3 people? (You’d need any multiple of 3, such as 3, 6, 9 or 12 loonies.)
• For more advanced students, ask if they notice any patterns for how amounts can be divided evenly. (The number of people to divide by needs to be a common multiple of the amount: for example, $9 can be split 3 ways because 3 is a multiple of 9 (3, 6, 9). Therefore, three people would each get $3 each.

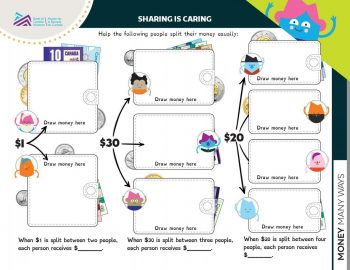
Have students complete the three questions on the next page. Show them that they can use the space next to the money to draw that amount in a different way if it makes splitting the money easier. Then, review the questions together.

Fair Share Fractions is an explainer for dividing money. Then take up Sharing is Caring for practice.

3.2.1 Taking it further

If time allows, give your students more hands-on practice:

• Show them how we regularly divide amounts when we play games. Arrange students in pairs or small groups. Provide each pair or group a small amount of play money and assign one student to be the “dealer.” That student will deal (divide) the money equally between their partner and themself or among the members in the group.
• For a more advanced activity, ask the students to roll two dice to help generate money math problems. The number from one die determines an amount of money in denominations of $10 (from 1, which equals $10, to 6, which equals $60). The other die determines how many [people will split that amount/parts to divide that amount into](from 1 to 6). Since not every combination of dollar amounts and [people/parts] can be solved with simple division, encourage students to re-roll if needed. Note any difficult dice combinations you’d like to solve as a class later (e.g., $30 [between four people/split into four parts] would require a mix of coins and bank notes).

Conclusion

Time

5 minutes

Review with students what they learned about expressing the same amount of money using different combinations of coins and bank notes. For example, ask if they remember how many nickels, dimes or quarters are needed to make up a dollar. Remind them of the relationship between fractions and money.

For homework, you may want to ask your students to practise dividing amounts of money with an adult, using either coins or bank notes. Or, the next time they are at a store, have them pay with the most accurate amount in cash they can and estimate how much change they will receive back.

Key takeaways

• Different combinations of coins and bank notes can represent the same amount of money.
• Modelling simple purchases can be useful for understanding everyday money transactions.
• Splitting—or dividing—money is a way of representing money in fractions.

Extensions

• Set up a role-play activity to practise paying and providing change. If you need some supplies, our Avatar Market activity includes templates of paper dolls and accessories for your students to set up their own market.
• Use our money and currency FAQ in a class discussion or for background information on the origins and types of Canadian money.
• Return to the money math fractions and the dollar equivalency [graphic/diagram] when introducing higher-level fractions, such as eighths.
• Introduce the idea of estimating taxes and how much something will cost with taxes added.